Aloittelijan opas binaaripuille

Jos olet käynyt tietotekniikan kurssin tietotekniikan tutkinnossa tai olet itseoppinut ohjelmoija, olet todennäköisesti törmännyt termiin "binaaripuut". Vaikka ne voivat kuulostaa hieman ylivoimaisilta ja monimutkaisilta, binaaripuun käsite on melko yksinkertainen.

Lue, kun leikkaamme binaaripuita ja miksi ne ovat välttämätön ydinkonsepti ohjelmoijille.

Mitä ovat binaaripuut?

Binaaripuut ovat yksi ensimmäisistä tietorakenteista, joita opiskelijoille opetetaan tietorakenteiden kurssilla. Binaaripuu koostuu monista solmuista, ja jokainen binaaripuun solmu sisältää kaksi osoitinta, jotka osoittavat vasemman ja oikean lapsisolmun.

Binaaripuun ensimmäistä solmua kutsutaan "juuriksi". Puun viimeisen tason solmuja kutsutaan lehdiksi.

Jokainen solmu sisältää tietoalueen ja kaksi solmukohdistinta. Tyhjää binaaripuuta edustaa nollaosoitin. Kuten olet ehkä jo ymmärtänyt, binaaripuilla voi olla vain kaksi lasta (tästä nimi).

Binaaristen puurakenteiden tyypit

Solmujen sijainnista riippuen on olemassa useita erilaisia ​​binääripuurakenteita. Binaaripuuta kutsutaan täydelliseksi binääripuuksi, kun puun jokaisella solmulla on joko nolla tai kaksi lasta. Täydellisessä binaaripuussa kaikilla solmuilla on kaksi lasta ja lehdet ovat kaikki samalla syvyydellä.

Aiheeseen liittyviä: Paras tapa oppia koodaamaan ilmaiseksi

Täydellisessä binaaripuussa on solmut täytetty kaikilla tasoilla, viimeistä tasoa lukuun ottamatta. Täydellisissä binaaripuissa solmut keskittyvät juuren vasemmalle puolelle. Toinen yleinen rakenne on tasapainoinen binääripuu; tässä rakenteessa oikean ja vasemman osapuun korkeuden on oltava korkeintaan yksi. Lisäksi vaaditaan, että vasen ja oikea osapuu on tasapainotettava.

On tärkeää huomata, että tasapainoisen binääripuun korkeus on O (logn), missä n on puun solmujen lukumäärä.

Joissakin tapauksissa, jos jokaisella solmulla on vain yksi vasen tai oikea lapsi, binaaripuusta voi tulla vinossa binääripuu. Sitten se käyttäytyy kuin linkitetty luettelo, tällaisia ​​puita kutsutaan myös rappeutuneeksi puuksi.

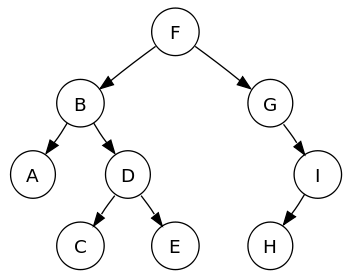
Mitä ovat binaariset hakupuut?

Binaarinen hakupuu (BST) on lähinnä tilattu binääripuu, jolla on erityisominaisuus, joka tunnetaan nimellä "binary search tree". BST -ominaisuus tarkoittaa, että solmut, joiden avainarvo on pienempi kuin juuri, sijoitetaan vasempaan osapuuhun, ja solmut, joiden avainarvo on suurempi kuin juuri, ovat osa oikeaa alipuuta.

BST -ominaisuuden on oltava totta jokaisessa puun seuraavassa solmusolmussa.

Binaariset hakupuut tarjoavat nopean lisäyksen ja haun. Lisäys-, poistamis- ja hakutoiminnot ovat pahimmassa tapauksessa O (n), joka on samanlainen kuin linkitetty luettelo.

Binaaripuiden edut

Binaaripuilla on monia etuja, minkä vuoksi ne ovat edelleen erittäin hyödyllinen tietorakenne. Niiden avulla voidaan näyttää tietojoukon rakenteelliset suhteet ja hierarkiat. Vielä tärkeämpää on, että binääripuut mahdollistavat tehokkaan haun, poistamisen ja lisäämisen.

Binääripuun käyttöönotto ja ylläpito on myös erittäin helppoa. Binääripuu tarjoaa ohjelmoijille järjestetyn taulukon ja linkitetyn luettelon edut; haku binääripuusta on yhtä nopeaa kuin lajitellussa taulukossa ja lisäys- tai poistotoiminnot ovat yhtä tehokkaita kuin linkitetyissä luetteloissa.

Binaaripuut ovat tärkeitä tietorakenteita

Binaaripuut ovat erittäin tärkeä tietorakenne, ja on ratkaisevan tärkeää, että ohjelmoijat voivat soveltaa niitä ohjelmiinsa. Usein haastattelijat kysyvät yksinkertaisia ​​binaaripuuongelmia, kuten läpikulkuja, suurinta syvyyttä, peilausta jne.

Suosittelemme, että ymmärrät binaaripuun käsitteen ja tunnet tyypilliset haastatteluongelmat.

TreeViz: Yksinkertainen tapa visualisoida tietorakenteita

Lue seuraava

Kirjailijasta