7 algoritmia, jotka jokaisen ohjelmoijan tulisi tietää

Ohjelmoinnin opiskelijana olet todennäköisesti oppinut paljon erilaisia ​​algoritmeja urasi aikana. Eri algoritmien hallitseminen on ehdottoman välttämätöntä jokaiselle ohjelmoijalle.

Niin monen algoritmin avulla voi olla haastavaa seurata olennaista. Jos valmistaudut haastatteluun tai vain harjaat taitojasi, tämä luettelo tekee siitä suhteellisen helppoa. Lue, kun luettelemme ohjelmoijille tärkeimmät algoritmit.

1. Dijkstran algoritmi

Edsger Dijkstra oli aikansa vaikutusvaltaisimpia tietotekniikan tutkijoita, ja hän osallistui siihen monilla eri laskentatieteen aloilla, mukaan lukien käyttöjärjestelmät, kääntäjärakentaminen ja paljon muuta lisää. Yksi Dijkstran merkittävimmistä panoksista on hänen lyhyimmän reittialgoritminsa kekseliäisyys, joka tunnetaan myös nimellä Dijkstran lyhin polkualgoritmi.

Dijkstran algoritmi löytää kaavion lyhyimmän polun lähteestä kaikkiin kuvaajan kärkiin. Jokaiseen algoritmin iterointiin lisätään kärki, jonka minimietäisyys lähteestä on sellainen, jota ei ole nykyisellä lyhyimmällä polulla. Tämä on ahne ominaisuus, jota Djikstran algoritmi käyttää.

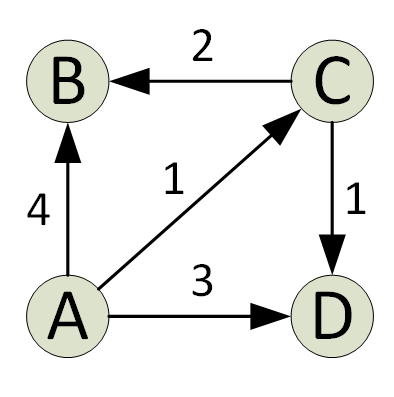
Algoritmi toteutetaan tyypillisesti käyttämällä sarjaa. Dijkstran algoritmi on erittäin tehokas, kun se toteutetaan Min Heapilla; löydät lyhyimmän polun vain O (V+ElogV) -ajalla (V on pisteiden lukumäärä ja E on tietyn kaavion reunojen määrä).

Dijkstran algoritmilla on rajoituksensa; se toimii vain suunnatuissa ja suunnattomissa kaavioissa, joiden reunat ovat positiivisia. Negatiivisille painoille Bellman-Ford-algoritmi on tyypillisesti parempi.

Haastattelukysymykset sisältävät yleensä Djikstran algoritmin, joten suosittelemme ymmärtämään sen monimutkaisia ​​yksityiskohtia ja sovelluksia.

2. Yhdistä lajittelu

Tässä luettelossa on pari lajittelualgoritmia, ja yhdistämislajittelu on yksi tärkeimmistä algoritmeista. Se on tehokas lajittelualgoritmi, joka perustuu Divide and Conquer -ohjelmointitekniikkaan. Pahimmassa tapauksessa yhdistämislajittelu voi lajitella n-numerot vain O (nlogn) -ajalla. Verrattuna primitiivisiin lajittelutekniikoihin, kuten Kuplan lajittelu (se vie O (n^2) aikaa), yhdistämislaji on erittäin tehokas.

Aiheeseen liittyviä: Johdatus yhdistämislajittelualgoritmiin

Yhdistämislajittelussa lajiteltava matriisi jaetaan toistuvasti osajoukkoihin, kunnes kukin aliryhmä koostuu yhdestä numerosta. Rekursiivinen algoritmi yhdistää sitten toistuvasti alijoukkoja ja lajittelee taulukon.

3. Pikavalinta

Quicksort on toinen Divide and Conquer -ohjelmointitekniikkaan perustuva lajittelualgoritmi. Tässä algoritmissa elementti valitaan ensin pivotiksi ja koko taulukko osioidaan tämän pivotin ympärille.

Kuten olet todennäköisesti arvannut, hyvä nivel on ratkaiseva tehokkaan lajittelun kannalta. Pivot voi olla joko satunnainen elementti, mediaelementti, ensimmäinen elementti tai jopa viimeinen elementti.

Pikavalinnan toteutukset vaihtelevat usein siinä, miten ne valitsevat kääntöpisteen. Keskimääräisessä tapauksessa quicksort lajittelee suuren taulukon hyvällä kääntöpisteellä vain O (nlogn) -ajalla.

Pikavalinnan yleinen pseudokoodi osioi taulukon toistuvasti pivotissa ja sijoittaa sen alirivin oikeaan paikkaan. Se myös sijoittaa elementit, jotka ovat pienempiä kuin kääntöpiste vasemmalle, ja elementit, jotka ovat suurempia kuin nivel oikealle.

4. Syvyys ensimmäinen haku

Syvyys ensimmäinen haku (DFS) on yksi ensimmäisistä opiskelijoille opetetuista kuvaajaalgoritmeista. DFS on tehokas algoritmi, jota käytetään kuvaajan siirtymiseen tai hakuun. Sitä voidaan myös muokata käytettäväksi puiden läpikulussa.

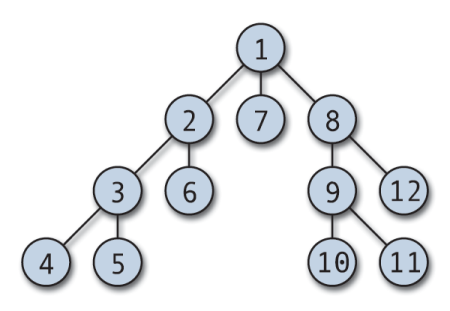
DFS -läpivienti voi alkaa mistä tahansa mielivaltaisesta solmusta ja sukeltaa jokaiseen viereiseen huippuun. Algoritmi perääntyy, kun ei ole vierailtua kärkeä tai on umpikuja. DFS toteutetaan tyypillisesti pinolla ja boolen matriisilla, jolla seurataan vierailtuja solmuja. DFS on yksinkertainen toteuttaa ja poikkeuksellisen tehokas; se toimii (V+E), missä V on kärkien lukumäärä ja E on reunojen lukumäärä.

DFS -läpikulun tyypillisiä sovelluksia ovat topologinen lajittelu, syklien havaitseminen kaaviossa, polun etsiminen ja vahvasti kytkettyjen komponenttien löytäminen.

5. Leveys-ensimmäinen haku

Leveys-ensimmäinen haku (BFS) tunnetaan myös puiden tasojärjestyksessä. BFS toimii O (V+E) -tilassa DFS -algoritmin tavoin. BFS käyttää kuitenkin jonoa pinon sijaan. DFS sukeltaa kuvaajaan, kun taas BFS kulkee kuvaajan leveyssuunnassa.

BFS -algoritmi käyttää jonoa pisteiden seurantaan. Vierailevissa vierekkäisissä kärkipisteissä vieraillaan, merkitään ja jonotetaan. Jos kärjessä ei ole viereistä kärkeä, piste poistetaan jonosta ja tutkitaan.

BFS: ää käytetään yleisesti vertaisverkoissa, painottamattoman kaavion lyhimmällä polulla ja pienimmän puun löytämiseksi.

6. Binaarihaku

Binaarihaku on yksinkertainen algoritmi tarvittavan elementin löytämiseksi lajitellusta taulukosta. Se toimii jakamalla taulukko toistuvasti puoliksi. Jos vaadittu elementti on pienempi kuin keskimmäinen elementti, keskielementin vasenta puolta käsitellään edelleen; Muussa tapauksessa oikea puoli puolitetaan ja etsitään uudelleen. Prosessi toistetaan, kunnes tarvittava elementti löytyy.

Binaarihaun pahimman ajan monimutkaisuus on O (logn), mikä tekee siitä erittäin tehokkaan lineaaristen matriisien etsinnässä.

7. Vähimmäispuitealgoritmit

Kaavion vähimmäispituuspuulla (MST) on vähimmäiskustannukset kaikkien mahdollisten ulottuvuuspuiden joukossa. Jousivan puun hinta riippuu sen reunojen painosta. On tärkeää huomata, että minimipituuspuita voi olla useita. MST -algoritmeja on kaksi, nimittäin Kruskal ja Prim.

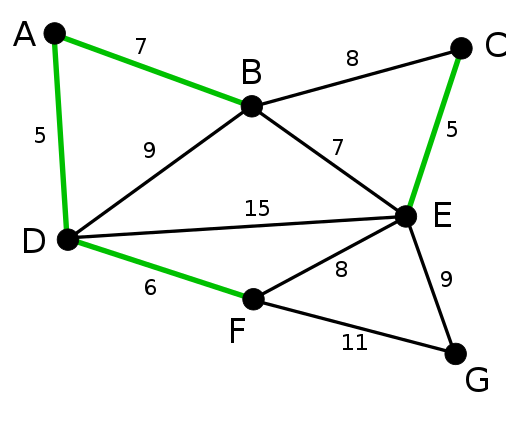
Kruskalin algoritmi luo MST: n lisäämällä reunan pienin kustannuksin kasvavaan joukkoon. Algoritmi lajittelee reunat ensin niiden painon mukaan ja lisää sitten reunat MST: hen alkaen minimistä.

On tärkeää huomata, että algoritmi ei lisää sykliä muodostavia reunoja. Kruskalin algoritmi on edullinen harvakaavioille.

Primin algoritmi käyttää myös ahneutta ja on ihanteellinen tiheille kaavioille. Primin MST: n keskeinen ajatus on kaksi erillistä kärkipisteitä; toinen joukko sisältää kasvavaa MST: tä, kun taas toinen sisältää käyttämättömiä kärkipisteitä. Jokaisessa iteroinnissa valitaan vähimmäispaino, joka yhdistää nämä kaksi sarjaa.

Vähimmäispituuspuun algoritmit ovat välttämättömiä klusterianalyysille, taksonomialle ja yleislähetysverkoille.

Tehokas ohjelmoija osaa algoritmeja

Ohjelmoijat oppivat ja kehittävät jatkuvasti taitojaan, ja on olemassa keskeisiä perusasioita, jotka kaikkien on oltava taitavia. Taitava ohjelmoija tuntee eri algoritmit, niiden edut ja haitat sekä sen, mikä algoritmi olisi sopivin tietylle skenaariolle.

Johdanto Shell -lajittelualgoritmiin

Vaikka kuoren lajittelu ei ole tehokkain tapa, aloittelijoilla on paljon hyötyä sen harjoittamisesta.

Lue seuraava

Kirjailijasta